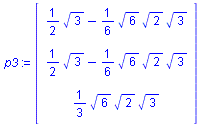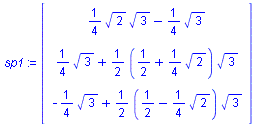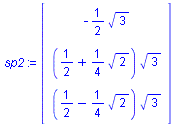Mathematik
von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel
(zu Kapitel 19: Analytische Geometrie)
Das Skalarprodukt
Der zentrale Begriff der euklidischen Geometrie ist das Skalarprodukt (inneres Produkt), dass in Maple beim Datentyp
vector
durch den Befehl
innerprod
aus dem Paket linalg berechnet wird.
| > |
u:=vector(4,[2,4,6,8]);
v:=vector(4,[-1,1,-1,1]);
with(linalg):
innerprod(u,v); |
Selbstverstaendlich koennnen wir das Skalarprodukt auch durch die Matrixmultiplikation ("Zeile mal Spalte") bestimmen. Dazu konvertieren wir v und w zunaechst auf den Datentyp
matrix
(beachten Sie, dass dadurch der Vektor wie im Buch als Spalte geschrieben wird) und berechnen
| > |
evalm(transpose(convert(u,matrix))&*convert(v,matrix)); |
Uebrigens durch Verwendung spitzer Klammern lassen sich Spaltenvektoren direkt eingeben, etwa
| > |
u:=<0,1,2-sqrt(3)>;
v:=<1,1,1>; |
Dieser Darstellung wird der Datentyp
Vector
(gross geschrieben!) zugeordnet, der im (neueren) Paket
LinearAlgebra
zur Linearen Algebra verwendet wird.
| > |
type(u,Vector);
type(u,vector);
type(u,matrix); |
Wir bleiben bei den Notationen des Pakets linalg (die Kommandos werden mit kleinen Anfangsbuchstaben geschrieben). Die euklidische Norm eines Vektors wird mit dem Befehl
norm
berechnet.
| > |
u:=convert(u,vector);
v:=convert(v,vector);
norm(v,2); |
Das zweite Argument in diesem Befehl ist notwendig, da auch andere Normen implementiert sind. So ist etwa mit
die Maximumsnorm gegeben.
Zur geometrischen Anschauung des Zusammenhangs zwischen Skalarprodukt, orthogonaler Projektion und dem Winkel normieren wir die beiden Vektoren
| > |
unorm:= evalm(scalarmul(u,1/norm(u,2)));
vnorm:= normalize(v); |
Dabei koennen wir entweder explizit mit dem Befehl
scalarmul
jedes Element mit dem Kehrwert der Norm des Vektors multiplizieren, oder wir nutzen den im Paket festgelegten Befehl
normalize
. Beide Varainten liefern dasselbe Ergebnis. Nun verschaffen wir uns ein 3D Bild der Situation. Berechnen wir zunaechst das Skalarprodukt von unorm und vnorm und den Winkel zwischen den beiden Vektoren.
| > |
projected:=evalf(innerprod(unorm,vnorm));
phi:=arccos(projected); |
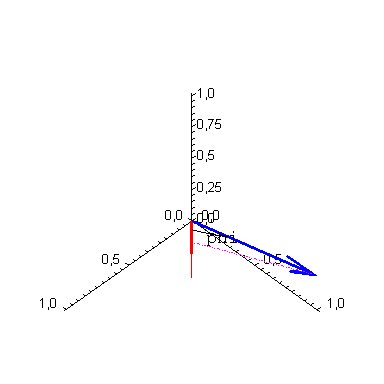
Damit verschaffen wir uns die Illustration
| > |
with(plots):
p1:=arrow(u,shape=arrow,color=blue):
p2:=arrow(v,shape=arrow,color=red):
p3:=arrow(unorm,shape=arrow,color=blue,thickness=2):
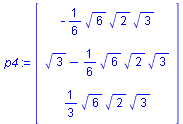
p4:=arrow(vnorm,shape=arrow,color=red,thickness=2):
p5:=spacecurve(evalm(unorm+t*(projected*vnorm - unorm)), t=0..1,linestyle="dot",color=magenta):
p6:=spacecurve(evalm(0.3*cos(t)*vnorm+0.3*sin(t)*normalize(unorm - projected*vnorm)),t=0..phi,color=black):
p7:=textplot3d([0.13,0.37,0.23,'phi'],font=[COURIER,14],color=black):
display(p1,p2,p3,p4,p5,p6,p7,scaling=constrained,axes=normal); |
Beachten Sie, dass wir uns den Winkel mit dem Befehl
spacecurve
zeichnenlassen, indem wir mit 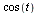 und
und 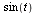 passende Linerakombinationen der beiden Vektoren vnorm und dem dazu senkrechten normalisierten Vektor in Richtung unorm - projected*vnorm betrachten.
passende Linerakombinationen der beiden Vektoren vnorm und dem dazu senkrechten normalisierten Vektor in Richtung unorm - projected*vnorm betrachten.
Fuer den Datentyp vector mit drei Komponenten ist auch das Kreuzprodukt durch einen eigenen Befehl verankert.
und mit
| > |
w:=vector(3,[-1,-1,1]);
innerprod(crossprod(u,v),w); |
berechnen wir gleich auch das Spatprodukt der drei Vektoren. Der Betrag dieses Werts entspricht, wie wir wissen, dem Volumen des durch die drei Vektoren aufgespannten Parallelepipeds.
| > |
with(plots):
p1:=arrow(u,shape=arrow,color=red):
p2:=arrow(v,shape=arrow,color=red):
p3:=arrow(w,shape=arrow,color=red):
p4:=spacecurve(evalm(u+t*v),t=0..1,color=blue):
p5:=spacecurve(evalm(v+t*u),t=0..1,color=blue):
p6:=spacecurve(evalm(u+t*w),t=0..1,color=blue):
p7:=spacecurve(evalm(w+t*u),t=0..1,color=blue):
p8:=spacecurve(evalm(v+t*w),t=0..1,color=blue):
p9:=spacecurve(evalm(w+t*v),t=0..1,color=blue):
p10:=spacecurve(evalm(u+v+t*w),t=0..1,color=blue):
p11:=spacecurve(evalm(u+w+t*v),t=0..1,color=blue):
p12:=spacecurve(evalm(v+w+t*u),t=0..1,color=blue):
display(p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,scaling=constrained,axes=normal); |
Wir verifizieren noch kurz, dass das Spatprodukt die Determinante der Matrix mit den drei Vektoren als Spalten (oder Zeilen) ist. Mit dem Befehl
concat
fuegen wir die drei Vektoren zu einer Matrix zusammen und erhalten
| > |
A:=concat(u,v,w);
det(A); |
Aspekte der analytischen Geometrie
Mit der Hesseschen Normalenform lassen sich Ebenen im Anschauungsraum leicht beschreiben. Betrachten wir etwa, die Ebene senkrecht zu n=(1,1,1)^T, mit dem Abstand k=1. Also liegen alle Punkte p auf E, fuer die das Skalarprodukt mit dem normierten Vektor
| > |
n:= convert(normalize(vector(3,[1,1,1])),matrix); |
Eins ergibt. Um moeglichst nah an der ueblichen Notation wie im Lehrbuch zu bleiben, wechseln wir zur Darstellung der Vektoren im Matrizenkalkuel, also als Spalten.
Wir pruefen leicht nach, dass etwa der Vektor
| > |
v:= matrix(3,1,[3,2,1])/2/sqrt(3); |
in der Ebene E liegt, da
| > |
evalm(transpose(n)&*v); |
gilt.
Mit Hilfe des Eniheitsnormalenvektors lassen sich nun auch die orthogonale Projektion und die Spiegelung eines Punkts an der Ebene bestimmen. Betrachten wir den Punkt
| > |
p:=matrix(3,1,[1,2,3]); |
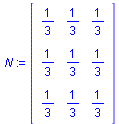
Wir berechnen das dyadische Produkt und belegen E3 mit der Einheitsmatrix.
| > |
N:= evalm(n &* transpose(n));
E3:=diag(1,1,1); |
Nun ergibt sich der gespiegelte Punkt aus
| > |
sp:=evalm(2*n+(E3-2*N)&*p); |
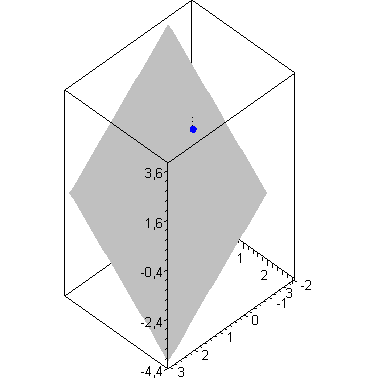
Ein 3D Bild dieser Situation erhalten wir durch
| > |
with(plots):
with(plottools):
g:=unapply(1/n[3,1]*(1-n[1,1]*x1-n[2,1]*x2),x1,x2);
pl1:=plot3d(g,-1..3,-1..3,color=gray,style=patchnogrid,axes=boxed,scaling=constrained):
pl2:=sphere([seq(p[j,1],j=1..3)],0.1,style=patchnogrid,color=blue):
pl3:=sphere([seq(sp[j,1],j=1..3)],0.1,style=patchnogrid,color=red):
pl4:=line([seq(p[j,1],j=1..3)],[seq(sp[j,1],j=1..3)],linestyle=2,color=black):
display(pl1,pl2,pl3,pl4); |
Nun wollen wir noch die Ebene um eine Drehachse durch den Ursprung in Richtung
| > |
d:=matrix(3,1,[0,1,1]); |
und den Winkel 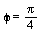 drehen. Dazu normieren wir den Richtungsvektor, geben die schiefsymmetrische Matrix Sd zur Darstellung des Kreuzprodukts mit d ein und berechnen die Drehmatrix wie auf Seite 657
drehen. Dazu normieren wir den Richtungsvektor, geben die schiefsymmetrische Matrix Sd zur Darstellung des Kreuzprodukts mit d ein und berechnen die Drehmatrix wie auf Seite 657
| > |
phi := Pi/4;
d := convert(normalize(convert(d,vector)),matrix);
tmp := evalm(convert(d,matrix)&*transpose(convert(d,matrix)));
Sd := matrix(3,3,[[0,-d[3,1],d[2,1]],[d[3,1],0,-d[1,1]],[-d[2,1],d[1,1],0]]);
Rd := evalm(tmp + cos(phi)*(E3-tmp) + sin(phi)*Sd); |
Die gedrehten Punkte ergeben sich aus einer Multiplikation mit der Matrix Rd. Also erhalten wir fuer die gedrehte Ebene den Normalenvektor
Weiter benoetigen wir noch den Abstand der gedrehten Ebene zum Ursprung. Da wir aber um den Ursprung drehen, bleibt dieser Abstand gleich. Dies pruefen wir, indem wir einen beliebigen Punkt aus der urspruenglichen Ebene waehlen, drehen diesen und bilden das Sklaraprodukt mit den neuen Normalenvektor. Wir nutzen den oben schon getesteten Vektor v und erhalten
| > |
sk := evalm(transpose(sn) &* (Rd &* v));
sk := evalf(sk[1,1]); |
Anschaulich wird die Drehung leicht deutlich. Zum Plot nutzen wir wieder die Normaldarstellung der gedrehten Ebene, 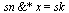 , bzw. die Funktion
, bzw. die Funktion
| > |
sg:=unapply(evalf(1/sn[3,1]*(sk-sn[1,1]*x1-sn[2,1]*x2)),x1,x2); |
berechnen ein paar Punkte auf den Ebenen
| > |
p1:= matrix(3,1,[1/2*sqrt(3),1/2*sqrt(3),0]);
p2:= matrix(3,1,[0,sqrt(3),0]);
tmp:=crossprod(convert(p1,vector)-convert(p2,vector),convert(n,vector)):
tmp:=normalize(tmp):
p3:= evalm(p1+sqrt(6)*convert(tmp,matrix));
p4:= evalm(p3 + (p2 -p1) );
sp1:=evalm(Rd&*p1);
sp2:=evalm(Rd&*p2);
sp3:=evalm(Rd&*p3);
sp4:=evalm(Rd&*p4);
|
und erhalten
| > |
pl1:=plot3d(g,-1..3,-1..3,color=gray,style=patchnogrid,axes=boxed):
pl2:=plot3d(sg,-1..3,-1..3,color=red,style=patchnogrid,axes=boxed):
pl3:=line([seq(-d[j,1],j=1..3)],[seq(4*d[j,1],j=1..3)],thickness=2,color=black):
pl4:=line([seq(p1[j,1],j=1..3)],[seq(p2[j,1],j=1..3)],color=magenta):
pl5:=line([seq(p1[j,1],j=1..3)],[seq(p3[j,1],j=1..3)],color=magenta):
pl6:=line([seq(p3[j,1],j=1..3)],[seq(p4[j,1],j=1..3)],color=magenta):
pl7:=line([seq(p4[j,1],j=1..3)],[seq(p2[j,1],j=1..3)],color=magenta):
pl8:=line([seq(sp1[j,1],j=1..3)],[seq(sp2[j,1],j=1..3)],color=blue):
pl9:=line([seq(sp1[j,1],j=1..3)],[seq(sp3[j,1],j=1..3)],color=blue):
pl10:=line([seq(sp3[j,1],j=1..3)],[seq(sp4[j,1],j=1..3)],color=blue):
pl11:=line([seq(sp4[j,1],j=1..3)],[seq(sp2[j,1],j=1..3)],color=blue):
display(pl1,pl2,pl3,pl4,pl5,pl6,pl7,pl8,pl9,pl10,pl11); |
wobei die Drehachse schwarz eingezeichnet ist.
Aufgaben
1. Gegeben ist die Gerade G, die durch die Parameterdarstellung x = (1,0,3)^T + t (1,0,-2)^T mit t in RR beschrieben wird, sowie die Punkte p = (7,11,0)^T und q = (6,12,-1)^T.
Bestimmen Sie die Gerade H durch p und q und die Gerade, die G und H senkrecht schneidet. Weiter geben Sie eine Darstellung der Ebene an, die parallel zu beiden Geraden liegt und von beiden denselben Abstand hat.
Loesung
2. Schreiben Sie ein Programm, dass die Position einer Baggerschaufel berechnet, wenn Sie die drei Gelenke mit den Winkel 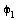 ,
, 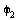 ,
, 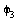 steuern.
steuern.
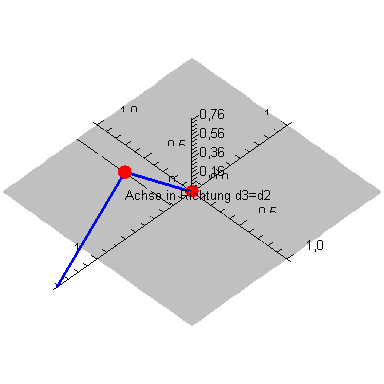
Dabei soll davon ausgegangen werden, dass sich der Arm aus zwei Stuecken der Laenge 1 zusammensetzt, die mit einem Gelenk verbunden sind und am Ursprung ansetzen. Am Ursprung befinden sich zwei Gelenke. Das eine dreht mit einem Winkel 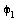 um die Achse
um die Achse 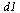 = (0,0,1)^T und das zweite Gelenk dreht, wenn
= (0,0,1)^T und das zweite Gelenk dreht, wenn 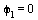 ist, um die Achse d2 = (0,-1,0)^T mit Winkel
ist, um die Achse d2 = (0,-1,0)^T mit Winkel 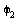 . Beachten Sie die Orientierung des Richtungsvektors, damit mit positiven Winkel
. Beachten Sie die Orientierung des Richtungsvektors, damit mit positiven Winkel 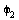 nach oben gedreht wird. Diese Achse aendert sich aber durch Drehung des ersten Gelenks um
nach oben gedreht wird. Diese Achse aendert sich aber durch Drehung des ersten Gelenks um 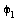 . Genauso ist am Verbindungspunkt der beiden Armstuecke ein drittes Gelenk, dass um dieselbe Achse
. Genauso ist am Verbindungspunkt der beiden Armstuecke ein drittes Gelenk, dass um dieselbe Achse 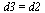 mit einem Winkel
mit einem Winkel 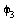 dreht (siehe Abbildung).
dreht (siehe Abbildung).
| > |
with(plots): with(plottools):
g:=(x1,x2)->0:
pl1:=plot3d(g,-1..1,-1..1,color=gray,style=patchnogrid,axes=normal,scaling=constrained):
pl2:=line([0,0,0],[1/sqrt(2),0,1/sqrt(2)],thickness=2,color=blue):
pl3:=line([1/sqrt(2),0,1/sqrt(2)],[sqrt(2),0,0],thickness=2,color=blue):
pl4:=sphere([0,0,0],0.05,style=patchnogrid,color=red):
pl5:=sphere([1/sqrt(2),0,1/sqrt(2)],0.05,style=patchnogrid,color=red):
pl6:=line([1/sqrt(2),-0.5,1/sqrt(2)],[1/sqrt(2),0.5,1/sqrt(2)],color=black,linestyle=5):
pl7:=textplot3d([[0.8,0.1,0.6,"Achse in Richtung d3=d2"]],color=black,align=right):
display(pl1,pl2,pl3,pl4,pl5,pl6,pl7); |
 |
Das Programm soll in Abhaengigkeit von den drei Winkeln 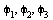 die zugehoerige affin lineare Abbildung liefern, also eine Matrix A und eine Translation p, sodass durch
die zugehoerige affin lineare Abbildung liefern, also eine Matrix A und eine Translation p, sodass durch 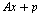 die neue Position jedes Punkts im Raum nach dieser Bewegung berechnet werden kann. Insbesondere muss gelten: fuer phi=(0,0,0)^T ist
die neue Position jedes Punkts im Raum nach dieser Bewegung berechnet werden kann. Insbesondere muss gelten: fuer phi=(0,0,0)^T ist 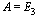 und p = (0,0,0)^T und fuer
und p = (0,0,0)^T und fuer 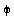 = (0,
= (0,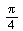 ,
,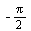 ) und dem Endpunkt x = (2,0,0)^T des Arms ist
) und dem Endpunkt x = (2,0,0)^T des Arms ist 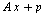 = (
= (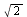 ,0,0)^T, wie in der Abbildung angedeutet.
,0,0)^T, wie in der Abbildung angedeutet.
Loesung
](images/kapitel-19maple_5.gif)
](images/kapitel-19maple_6.gif)
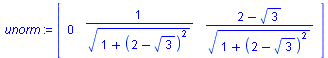
![]() und
und ![]() passende Linerakombinationen der beiden Vektoren vnorm und dem dazu senkrechten normalisierten Vektor in Richtung unorm - projected*vnorm betrachten.
passende Linerakombinationen der beiden Vektoren vnorm und dem dazu senkrechten normalisierten Vektor in Richtung unorm - projected*vnorm betrachten. 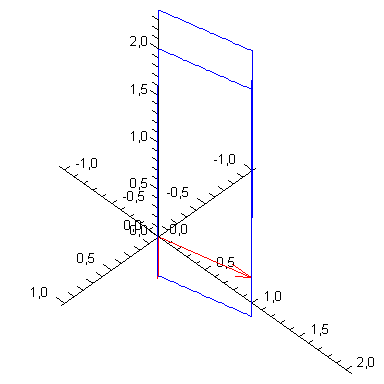
![array( 1 .. 3, 1 .. 3, [( 3, 3 ) = 1, ( 3, 2 ) = 1, ( 2, 3 ) = -1, ( 3, 1 ) = `+`(2, `-`(`*`(`^`(3, `/`(1, 2))))), ( 1, 1 ) = 0, ( 2, 1 ) = 1, ( 1, 3 ) = -1, ( 2, 2 ) = 1, ( 1, 2 ) = 1 ] )](images/kapitel-19maple_25.gif)
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = `+`(`*`(`/`(1, 3), `*`(`^`(3, `/`(1, 2))))), ( 1, 1 ) = `+`(`*`(`/`(1, 3), `*`(`^`(3, `/`(1, 2))))), ( 2, 1 ) = `+`(`*`(`/`(1, 3), `*`(`^`(3, `/`(1, 2))))) ] )](images/kapitel-19maple_27.gif)
![`+`(`*`(`/`(1, 6), `*`(array( 1 .. 3, 1 .. 1, [( 3, 1 ) = 1, ( 1, 1 ) = 3, ( 2, 1 ) = 2 ] ), `*`(`^`(3, `/`(1, 2))))))](images/kapitel-19maple_28.gif)
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = 3, ( 1, 1 ) = 1, ( 2, 1 ) = 2 ] )](images/kapitel-19maple_30.gif)
![array( 1 .. 3, 1 .. 3, [( 3, 3 ) = 1, ( 1, 1 ) = 1, ( 2, 2 ) = 1 ] )](images/kapitel-19maple_32.gif)
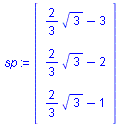
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = 1, ( 1, 1 ) = 0, ( 2, 1 ) = 1 ] )](images/kapitel-19maple_36.gif)
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = `+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2))))), ( 1, 1 ) = 0, ( 2, 1 ) = `+`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2))))) ] )](images/kapitel-19maple_39.gif)
![array( 1 .. 3, 1 .. 3, [( 3, 3 ) = `/`(1, 2), ( 3, 2 ) = `/`(1, 2), ( 2, 3 ) = `/`(1, 2), ( 3, 1 ) = 0, ( 1, 1 ) = 0, ( 2, 1 ) = 0, ( 1, 3 ) = 0, ( 2, 2 ) = `/`(1, 2), ( 1, 2 ) = 0 ] )](images/kapitel-19maple_40.gif)
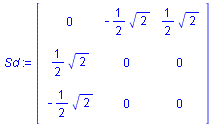
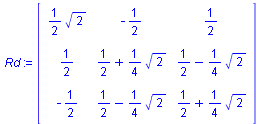
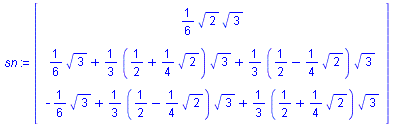
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = 0, ( 1, 1 ) = `+`(`*`(`/`(1, 2), `*`(`^`(3, `/`(1, 2))))), ( 2, 1 ) = `+`(`*`(`/`(1, 2), `*`(`^`(3, `/`(1, 2))))) ] )](images/kapitel-19maple_52.gif)
![array( 1 .. 3, 1 .. 1, [( 3, 1 ) = 0, ( 1, 1 ) = 0, ( 2, 1 ) = `*`(`^`(3, `/`(1, 2))) ] )](images/kapitel-19maple_53.gif)