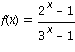kapitel-07maple.html

Mathematik

von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel

(zu Kapitel 7: Stetige Funktionen)

> restart;

Stetige und unstetige Funktionen

Im Worksheet zu Kapitel 4 haben wir schon gesehen, wie Funktionen und Graphen in Maple realisiert sind. Lassen wir auch komplexe Argumente zu, so koennen wir die Graphen von Real- und Imaginaerteil getrennt als Flaechen ueber der komplexen Ebene darstellen. Zum Beispiel ergibt sich

> f:=z->(z+I)/(1+z^2);
plot3d(Im(f(x+I*y)),x=-2..2,y=-2..2,view=-2..2,axes=boxed);

Um abschnittweise definierte Funktionen in das System einzugeben, kann der Befehl piecewise genutzt werden.

> piecewise(x>=1,x^2-2*x+2,(x<1 and x>=0), x^4+1/2*x^3-1/2*x^2,x<0,1/2*x+1);
f:=unapply(%,x);

Beachten Sie die Syntax des Befehls: es wird im Wechsel eine Bedingung an x und der Ausdruck fuer die Funktion bei dieser Bedingung eingegeben. Intervalle, auf denen keine Angaben gemacht werden, werden automatisch auf 0 gesetzt.

Um den Graphen der Funktion anzusehen, ohne stoerende Verbindungslinien, muessen wir dem Befehl plot noch mitteilen, dass die gezeigten Funktionen unstetig sein koennen. Dazu dient die Variable discont .

> plot(f,-2..2,discont=true);

Betrachten wir die Grenzwerte von links und von rechts gegen , so haben wir die Unstetigkeit der Funktion an dieser Stelle explizit geprueft.

> assume(x>0);
limit(f(x),x=0);

> assume(x<0);
limit(f(x),x=0);

Um geschlossene Ausdruecke zu Umkehrfunktionen zu bekommen, versuchen wir den solve Befehl zu nutzen. Es ergibt sich etwa

> f:= x-> (x+1)/(1-x);
g:= solve(y=f(x),x);

Also ist mit : R\{-1} -> R eine Umkehrfunktion zu : R\ {1} -> R gegeben, was wir durch

> x := 'x';
g:=unapply(g,y);
simplify(f(g(y)));
simplify(g(f(x)));

bestaetigen.

Die Bestimmung eines Ausdrucks fuer eine Umkehrfunktion erfordert Gleichungen der Form zu loesen. Dies ist nicht immer explizit moeglich, wie wir an verschiedenen Stellen schon gesehen haben. Numerisch koennen wir aber mit dem Bisektionsverfahren bei vorgegebenen Wert und einer stetigen Funktion eine Loesung ermitteln. Ohne weitere Einschraenkungen setzen wir und suchen Nullstellen einer Funktion .

Wir schreiben ein kurzes Programm, dass das Bisektionsverfahren ausfuehrt.

> bisekappr := proc(f,a,b,N)
local i, xa, xb, xm, fa, fb, fm, eps;
global intervall, nullstelle;
xa := a;
xb := b;
fa := evalf(f(xa));
fb := evalf(f(xb));
eps       := 10^(-8);

if fa*fb>eps then
   print("kein Vorzeichenwechsel zwischen f(a) und f(b)");
else
  intervall := [xa,xb];
  print(intervall);
  for i to N do
     xm := 0.5 * (xa + xb);
     fm := f(xm);
     if fa*fm>eps then
        xa := xm;
        fa := fm;
     elif fa*fm<eps then
        xb := xm;
        fb := fm;
     else
       nullstelle := 0.5*(xa+xb);
       print(nullstelle);
       break;
     end if;
     print([xa,xb]);
  od;
end if;
end:

Nun nutzen wir unseren Algorithmus, um Nullstellen zu approximieren. Betrachten wir etwa das Polynom p mit

> p:= x-> x^5+3*x^3-x^2+1;

Wir suchen zunaechst ein Startintervall:

> p(-1); p(0); p(1);

Nach dem Zwischenwertsatz gibt es mindestens eine Nullstelle im Intervall [-1,0] und mit dem Bisektionsverfahren koennen wir eine Nullstelle einschachteln:

> bisekappr(p,-1,0,10);

Aufgaben

(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)

1. Die Graphen der beiden Funktionen mit