kapitel-10maple.mw
Mathematik
von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel
(zu Kapitel 10: Differenzialrechnung)
Ableitungen
Zum Differenzieren von Funktionen ist der Operator
D
definiert. Also koennen wir zu einer Funktion, zum Beispiel
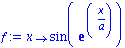
die Ableitungsfunktion durch
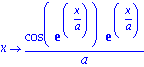
berechnen lassen.
Um Ausdruecke nach bestimmten Variablen zu differenzieren, gibt es den Befehl
diff
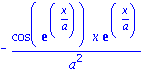
Das zweite Argument im Befehl muss den Namen der Varaible enthalten, nach der differenziert werden soll.
Nun koennen wir eine Kurvendiskussion durchfuehren zum Beispiel mit  .
.
| > |
f1:=unapply(subs(a=1,f(x)),x); |
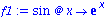
Das Symbol
@
bezeichnet die Komposition von Operatoren (Funktionen).
Zunaechst suchen wir Nullstellen der Funktion.
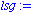
Es wird keine Nullstelle gefunden. Aber Vorsicht: es existieren Nullstellen! In diesem Beispiel kann Maple alle Nullstellen finden, wenn wir erlauben, dass nach mehreren Loesungen gesucht wird. Dazu ist
| > |
_EnvAllSolutions := true: |
zu setzen. Jetzt erhalten wir
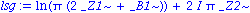
Es ist wichtig zu beruecksichtigen, dass Maple stets im Koerper der komplexen Zahlen rechnet (wenn keine Voraussetzungen gemacht sind). Maple hat drei Hilfsvariablen eingefuehrt. Diese sind aber nicht beliebig waehlbar, was durch den Zusatz ~ angezeigt ist. Welche Bedingungen an die Variablen gesetzt sind, koennen wir uns mit
about
anzeigen lassen. Dazu lassen sich die unbekannten Groessen mit dem Befehl
indets
aus dem Ausdruck lesen.
{_Z2, _Z1, _B1, ln(Pi*(2*_Z1+_B1))}:
is used in the following assumed objects
[_Z2] assumed integer
[_B1] assumed OrProp(0,1)
[_Z1] assumed integer
Wichtig ist noch das asymptotische Verhalten der Funktion fuer  oder
oder  .
.
| > |
limit(f1(x),x=-infinity); limit(f1(x),x=infinity); |


Der zweite Grenzwert existiert nicht. Aber Maple gibt hier das Grenzintervall an von allen Werten, die Grenzwert sein koennen bei entsprechend gewaehlten Folgen x_n.
Eine weitere Frage ist: Gibt es Extremalstellen, also Nullstellen der ertsen Ableitung?
| > |
lsg:=solve(D(f1)(x)=0,x);
about(indets(lsg)); |
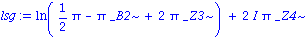
{_Z4, _Z3, _B2, ln(1/2*Pi-Pi*_B2+2*Pi*_Z3)}:
is used in the following assumed objects
[_Z4] assumed integer
[_Z3] assumed integer
[_B2] assumed OrProp(0,1)
Selbstverstaendlich koennen wir auch die zweite Ableitung betrachten.
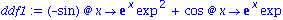
Beachten Sie, dass mit
@@
Potenzen von Operatoren kurz geschrieben werden koennen. D@@2 ist also nur eine andere Notation fuer den Befehl D(D(f1));
Mit
| > |
evalb( evalf(ddf1(ln(1/2*Pi))) < 0); |
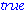
sehen wir, dass im ersten positiven Extremum ein Maximum der Funktion liegen muss.
Der Befehl
evalb
wertet einen Ausdruck logisch aus (Datentyp
boolean
).
Um hoehere Ableitungen von Ausdruecken zu bestimmen, gibt es folgende Modifikation des Befehls diff .
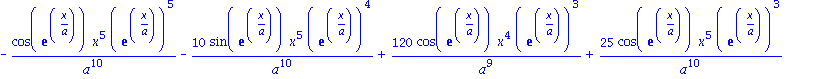
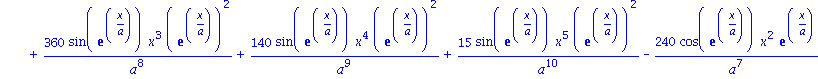
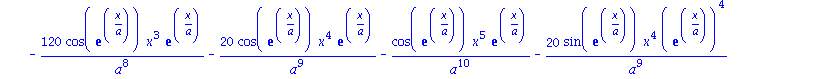
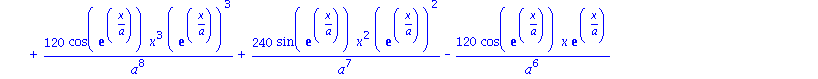
als Abkuerzung fuer diff(diff(diff(diff(diff(asdr,a),a),a),a),a);
Nun sehen wir uns noch den Graphen von f1 an.
![[Plot]](images/kapitel-10maple_19.gif)
Das Newton Verfahren
Verschiedene Moeglichkeiten nichtlineare Gleichungen zu loesen, sind inzwischen schon angeklungen. In maple uebernimmt der solve Befehl in den meisten Faellen diese Arbeit. Trotzdem wollen wir hier das Newton Verfahren genauer untersuchen. Versuchen wirzum Beispiel die Gleichung

im Intervall [0, /2] zu loesen, d.h. wir suchen Nullstellen der Funktion
/2] zu loesen, d.h. wir suchen Nullstellen der Funktion
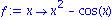
Betrachten wir den Graph der Funktion f, so ist ersichtlich, dass es im Intervall eine Nulstelle gibt.
| > |
with(plots): with(plottools):
p1:=plot(f(x),x=0..Pi/2,y=-1..1,color=blue,thickness=3, scaling=constrained):
p2:=circle([0.8241,0],0.04,color=red,thickness=3):
display(p1,p2); |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
![[Plot]](images/kapitel-10maple_23.gif)
Wir schreiben ein eigenes Programm, dass ausgehend von einem Startwert ![x[0]](images/kapitel-10maple_24.gif) einige Newton-Schritte durchfuehrt, um eine Nulstelle zu approximieren. Um eigene Prozeduren zu schreiben bietet Maple den Befehl
proc
. Mit
local
und global werden lokale oder globale Variablen definiert. Lokale Variablen exisitieren nur innerhalb des Programms. Globale Variablen bleiben nach Aufruf des Programms weiterhin belegt. Die ueblichen Programmierkonzepte, wie Schleifen (
while
,
for
) und bedingte Anweisungen (
if
) stehen selbstverstaendlich zur Verfuegung.
einige Newton-Schritte durchfuehrt, um eine Nulstelle zu approximieren. Um eigene Prozeduren zu schreiben bietet Maple den Befehl
proc
. Mit
local
und global werden lokale oder globale Variablen definiert. Lokale Variablen exisitieren nur innerhalb des Programms. Globale Variablen bleiben nach Aufruf des Programms weiterhin belegt. Die ueblichen Programmierkonzepte, wie Schleifen (
while
,
for
) und bedingte Anweisungen (
if
) stehen selbstverstaendlich zur Verfuegung.
| > |
newtappr := proc (f, x0, N)
local i, xn, fp;
global newsteps;
xn := x0;
fp := D(f);
newsteps := xn;
for i to N do
xn := evalf(simplify(xn-f(xn)/fp(xn)));
newsteps := newsteps, xn
od;
newsteps
end: |
Bemerkung: Um bei der Eingabe einen Zeilenumbruch zu erreichen, ohne, dass der Befehl ausgefuehrt wird, muss [Shift][Enter] verwendet werden.
Mit dem Startwert ![x[0] = 1](images/kapitel-10maple_25.gif) berechnen wir die ersten 10 Iterationsschritte:
berechnen wir die ersten 10 Iterationsschritte:
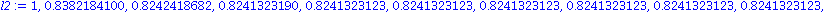

| > |
p1:=plot(f(x),x=0.6..1.1,y=-0.5..0.5,color=blue,scaling=constrained):
p2:=circle([l2[1],f(l2[1])],0.01,color=red,thickness=3):
p3:=plot(f(l2[1])+D(f)(l2[1])*(x-l2[1]),x=0.6..1.1,color=red,linestyle=DASH):
p4:=circle([l2[2],f(l2[2])],0.01,color=red,thickness=3):
p5:=plot(f(l2[2])+D(f)(l2[2])*(x-l2[2]),x=0.6..1,color=black,linestyle=DASH):
display(p1,p2,p3,p4,p5);
|
![[Plot]](images/kapitel-10maple_28.gif)
Mit dem Startwert ![x[0] = -Float(1, -1)](images/kapitel-10maple_29.gif) ergibt sich
ergibt sich
| > |
l2:=newtappr(f,-0.1,10); |
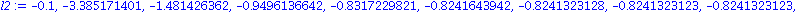

| > |
p1:=plot(f(x),x=-4..1,y=-3..3,color=blue,scaling=constrained):
p2:=circle([l2[1],f(l2[1])],0.01,color=red,thickness=3):
p3:=plot(f(l2[1])+D(f)(l2[1])*(x-l2[1]),x=-4..0.4,color=red,linestyle=DASH):
display(p1,p2,p3); |
![[Plot]](images/kapitel-10maple_32.gif)
Mit diesem Startwertkonvergiert das Verfahren somit gegen die zweite Nullstelle der Funktion.
Taylorpolynome
Zum Bestimmen eines Taylorpolynoms ist der Befehl
taylor
vorgesehen.
| > |
f:=x->1/(1+x);
p2:=taylor(f(x),x=0,3); |
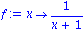
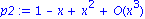
Das erste Argument enthaelt die Funktion in Form eines Ausdrucks. Das zweite Argument gibt die Variable und den Entwicklungspunkt an. Das dritte Argument ist die Anzahl der gewuenschten ausgewerteten Terme. Alle weiteren Terme von hoeherem Grad, also das Restgleid, werden im Landausymbol, hier O(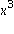 ), zusammengefasst.
), zusammengefasst.
Nun koennen wir uns die Approximation der Funktion durch die Taylorpolynome veranschaulichen. Zunaechst die Tangente (als Ausdruck)
| > |
p1:=taylor(f(x),x=0,2);
a1:=convert(convert(p1,polynom),exp); |
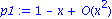
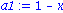
Und noch das zweite und das zehnte Taylorpolynom
| > |
a2:=convert(convert(p2,polynom),exp);
p10:=taylor(f(x),x=0,11):
a10:=convert(convert(p10,polynom),exp); |
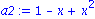
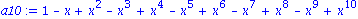
| > |
plot([f(x),a1,a2,a10],x=-0.5..0.5,color=[black,red,blue,green]); |
![[Plot]](images/kapitel-10maple_40.gif)
Beachten Sie, dass in komplizierteren Situationen nicht immer ein Taylorpolynom (von Maple) bestimmt werden kann. Wir haben das wichtige Beispiel einer stueckweise definierten Funktion (
piecewise
) im Buch vorgestellt, bei der die Taylorreihe nicht gegen die Funktion konvergiert.
| > |
f:=x->piecewise(x>0, exp(-1/x));
plot(f,-0.5..0.5); |
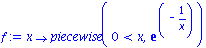
![[Plot]](images/kapitel-10maple_42.gif)
Error, (in series/exp) unable to compute series
Auch der allgemeinere Befehl
series
, der wenn moeglich eine Taylorreihe bestimmt, nuetzt in solchen Faellen nichts.
Spline-Interpolation
Die Spline-Interpolation ist durch einen Befehl in Maple verankert. Betrachten wir etwa das Beispiel aus dem Buch, die Funktion mit
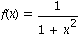
.
Belegen wir zwei Listen mit Stuetzstellen und den zugehoerigen Funktionswerten
| > |
xdaten:=[seq(j,j=-3..3)];
ydaten:=[seq(1/(1+j^2),j=-3..3)]; |
![xdaten := [-3, -2, -1, 0, 1, 2, 3]](images/kapitel-10maple_44.gif)
![ydaten := [1/10, 1/5, 1/2, 1, 1/2, 1/5, 1/10]](images/kapitel-10maple_45.gif)
so liefert uns der Befehl
spline
die stueckweise definierte Funktion
| > |
spline(xdaten,ydaten,t,linear); |
![PIECEWISE([2/5+1/10*t, t < -2], [4/5+3/10*t, t < -1], [1+1/2*t, t < 0], [1-1/2*t, t < 1], [4/5-3/10*t, t < 2], [2/5-1/10*t, otherwise])](images/kapitel-10maple_46.gif)
Das erste Argument listet die Stuetzstellen und das zweite Argument die Werte an diesen Stellen auf. Im dritten Argument wird der Variablenname fuer die Funktion festgelegt. Das vierte Argument des spline Befehls ist optional und legt den Grad der Polynome fest. Wenn nichts angegeben wird, wird ein natuerlicher kubischer Spline bestimmt. Zugelassen sind Zahlen 1,2,3, ... oder Namen wie linear, quadratic oder cubic fuer den letzten Parameter.
Wir sehen uns zunaechst den Graphen des linearen Splines an:
| > |
f:=x->1/(1+x^2);
g:=t->spline(xdaten,ydaten,t,linear);
plot([f(x),g(x)],x=-3..3,color=[black,red]); |
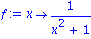

![[Plot]](images/kapitel-10maple_49.gif)
Fuer den entsprechenden natuerlichen kubischen Spline erhalten wir
| > |
g:=t->spline(xdaten,ydaten,t,3);
plot([f(x),g(x)],x=-3..3,color=[black,blue]); |
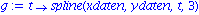
![[Plot]](images/kapitel-10maple_51.gif)
Der Befehl spline gehoert zum Paket
CurveFitting
, wird aber in den aktuellen Maple Versionen auch ohne laden des Pakets bereitgestellt. In diesem Paket finden wir auch den Befehl
PolynomialInterpolation
, der uns die in Kapitel 4 beschriebene Polynom Interpolation berechnet.
| > |
with(CurveFitting):
PolynomialInterpolation(xdaten,ydaten, t); |
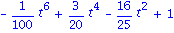
mit dem Graphen
| > |
g:=t->PolynomialInterpolation(xdaten,ydaten, t);
plot([f(t),g(t)],t=-3..3,color=[black,red]); |
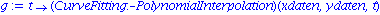
![[Plot]](images/kapitel-10maple_54.gif)
Mit der Option Lagrange besteht auch die Moeglichkeit, sich die Lagrange Darstellung des Interploationspolynoms zu beschaffen:
| > |
PolynomialInterpolation(xdaten,ydaten, t, form=Lagrange); |
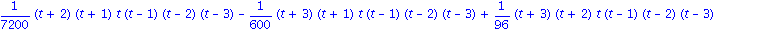
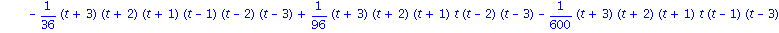

Aufgaben
(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)
1. Gegeben sei die Funktion

Bestimmen Sie den Definitionsbereich dieser Funktion, ihre Nullstellen, ihre Extremalstellen und das asymptotische Verhalten fuer wachsende Betraege von x.
Loesung
2. Berechnen Sie die Taylorpolynome der Ordnung 10 zu den angegebenen Funktionen um ![x[0] = 0](images/kapitel-10maple_59.gif) ;
;
 ,
,  ,
, 
Loesung
3. Schreiben Sie ein Programm, dass das Halley Verfahren aus Aufgabe 10.5 ausfuehrt und testen Sie Ihr Programm im Vergleich zum oben angegebenen Newton Verfahren, um je eine Nullstelle der beiden Funktionen mit
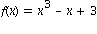 und Startwert
und Startwert ![x[0] = -1](images/kapitel-10maple_64.gif) bzw.
bzw. 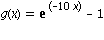 mit Startwert
mit Startwert ![x[0] = -1/2](images/kapitel-10maple_66.gif)
zu finden
Loesung
![]()
![]() .
.![]()
![]()
![]()
![]() oder
oder ![]() .
. ![]()
![]()
![]()
![]()
![]()
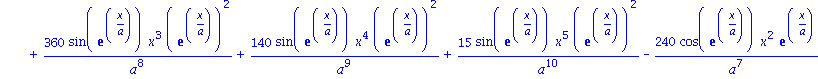
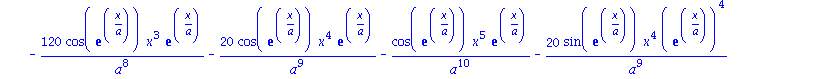
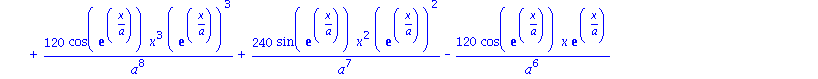
![[Plot]](images/kapitel-10maple_19.gif)
![[Plot]](images/kapitel-10maple_23.gif)
![[Plot]](images/kapitel-10maple_28.gif)
![[Plot]](images/kapitel-10maple_32.gif)
![[Plot]](images/kapitel-10maple_40.gif)
![[Plot]](images/kapitel-10maple_42.gif)
![PIECEWISE([2/5+1/10*t, t < -2], [4/5+3/10*t, t < -1], [1+1/2*t, t < 0], [1-1/2*t, t < 1], [4/5-3/10*t, t < 2], [2/5-1/10*t, otherwise])](images/kapitel-10maple_46.gif)
![[Plot]](images/kapitel-10maple_49.gif)
![[Plot]](images/kapitel-10maple_51.gif)
![[Plot]](images/kapitel-10maple_54.gif)